In mathematics, particularly in linear algebra [Linear algebra], matrix multiplication is a binary operation that produces a matrix [Matrix] from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices \(A\) and \(B\) is denoted as \(AB\).
[…]
If \(A\) is an \(m \times n\) matrix and \(B\) is an \(n \times p\) matrix,
\[ \mathbf{A} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix},\quad\mathbf{B} = \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1p} \\ b_{21} & b_{22} & \cdots & b_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{np} \\ \end{pmatrix} \]
the matrix product \(C = AB\) (denoted without multiplication signs or dots) is defined to be the \(m \times p\) matrix
\[ \mathbf{C} = \begin{pmatrix} c_{11} & c_{12} & \cdots & c_{1p} \\ c_{21} & c_{22} & \cdots & c_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ c_{m1} & c_{m2} & \cdots & c_{mp} \\ \end{pmatrix} \]
such that
\[ c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj} = \sum\limits_{k = 1}^{n}a_{ik}b_{kj} \]
for \(i = 1, \dots, m\) and \(j = 1, \dots, p\).
Matrix multiplication as a linear combination
Right-multiplication: combination of columns
Let’s begin by looking at the right-multiplication of matrix \(X\) by a column vector:
$$
\begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \\ \end{pmatrix}\begin{pmatrix} a \\ b \\ c \\ \end{pmatrix} = \begin{pmatrix} ax_1 & bx_2 & cx_3 \\ ay_1 & by_2 & cy_3 \\ az_1 & bz_2 & cz_3 \\ \end{pmatrix}
$$
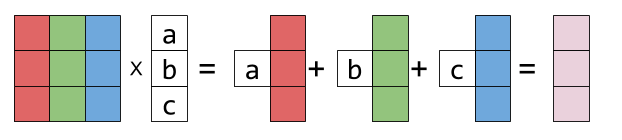
Representing the columns of X by colorful boxes will help visualize this:
Sticking the white box with a in it to a vector just means: multiply this vector by the scalar a. The result is another column vector - a linear combination of X’s columns, with a, b, c as the coefficients.
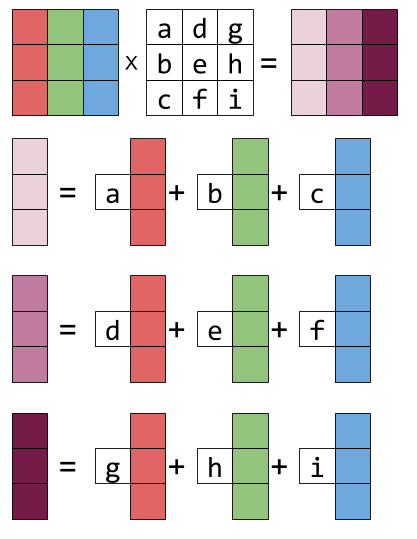
Right-multiplying X by a matrix is more of the same. Each resulting column is a different linear combination of X’s columns:
$$
\begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \\ \end{pmatrix}\begin{pmatrix} a & d & g \\ b & e & h \\ c & f & i \\ \end{pmatrix} = \begin{pmatrix} ax_1 + by_1 + cz_1 & dx_1 + ey_1 + fz_1 & gx_1 + hy_1 + iz_1 \\ ax_2 + by_2 + cz_2 & dx_2 + ey_2 + fz_2 & gx_2 + hy_2 + iz_2 \\ ax_3 + by_3 + cz_3 & dx_3 + ey_3 + fz_3 & gx_3 + hy_3 + iz_3 \\ \end{pmatrix}
$$
Graphically:
If you look hard at the equation above and squint a bit, you can recognize this column-combination property by examining each column of the result matrix.
Left-multiplication: combination of rows
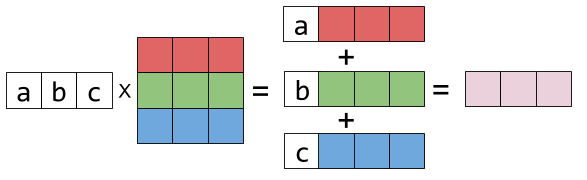
Now let’s examine left-multiplication. Left-multiplying a matrix X by a row vector is a linear combination of X’s rows:
$$
\begin{pmatrix} a & b & c \\ \end{pmatrix} \begin{pmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \\ \end{pmatrix} = \begin{pmatrix} ax_1 + bx_2 + cx_3 & ay_1 + by_2 + cy_3 & az_1 + bz_2 + cz_3 \\ \end{pmatrix}
$$
Is represented graphically thus:
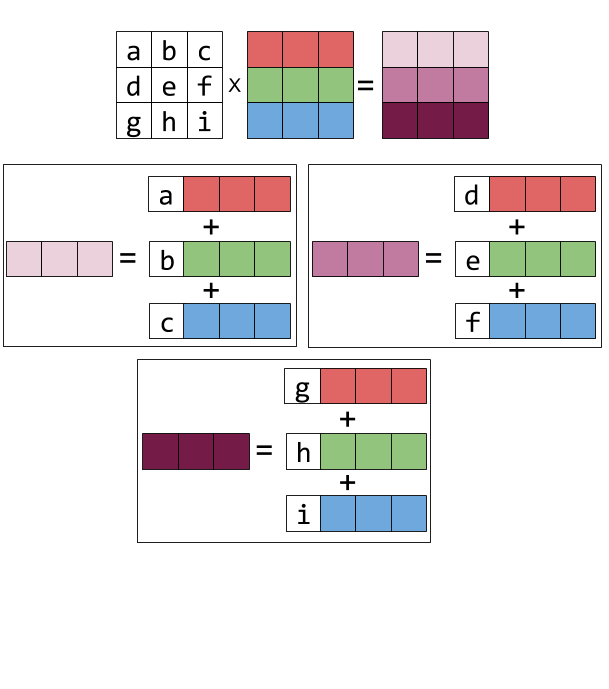
And left-multiplying by a matrix is the same thing repeated for every result row: it becomes the linear combination of the rows of X, with the coefficients taken from the rows of the matrix on the left. Here’s the equation form:
$$
\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{pmatrix} \begin{pmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \\ \end{pmatrix} = \begin{pmatrix} ax_1 + bx_2 + cx_3 & ay_1 + by_2 + cy_3 & az_1 + bz_2 + cz_3 \\ dx_1 + ex_2 + fx_3 & dy_1 + ey_2 + fy_3 & dz_1 + ez_2 + fz_3 \\ gx_1 + hx_2 + ix_3 & gy_1 + hy_2 + iy_3 & gz_1 + hz_2 + iz_3 \\ \end{pmatrix}
$$
And the graphical form: